Failure Modes and Models

When your machine collapses

How a machine achieves a goal can determine how it fails

I liked this provocative tweet:

For most ‘applications’, I’m not sure why people care so much about whether models are “just memorizing/recombining the train data.” If the model does what you want, why care about where the model came from?
(lots of disclaimers below)

— Preetum Nakkiran (@PreetumNakkiran) April 6, 2022

It’s a sentiment I’ve seen a lot¹. It’s also something I’ve semi-addressed before:

Failures modes - or how something fails - tells you an incredible amount about how something works.

Maybe there are 5 different designs that can all achieve the same function, but it's really hard to make 2 different designs that fail in the all the same ways.

— elsewhere (@affineincontrol) December 13, 2021

I wanted to illustrate this point more clearly here.

Models Achieve Goals

Models are machines that are meant to capture relationships. Science cares about relationships that we find in the real world². So it makes sense that good models matter in science.

The idea that some models are useful is important, because utility is how we chisel models into something that moves from predictive to insightful. At the end of the day, we want models that are both useful and insightful, but when it comes to applications we really only care about useful models… right?

Models make assumptions

The problem is that all models always make assumptions - namely in how they treat the “outside world”.

In the real world, you can’t just abstract away the outside world or assume it will always behave in the way you need it to for your model to hold. That means in the real world your model’s assumptions will be put to the test, maybe even broken. How the resulting broken model “works” depends heavily on its internal structure.

So the answet to the provocative tweet is simply: it matters a great deal.

Example: Two Models

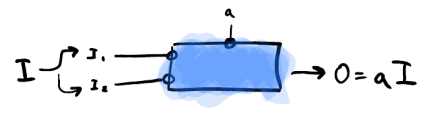I need a machine that takes an input and multiplies it by a fixed value. So let’s try to implement two different models that achieve the same goal.

Two models that achieve the same goal

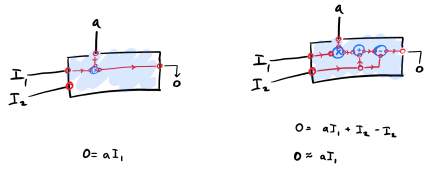
We have two models that accomplish the same goal: they take input 1 $ I_1 $ and they multiply it by a value $ a $. They also take a second input $ I_2 $ but, when the two models are working, that input doesn’t actually have any impact on the output.

So both models “work”, why should I care how they actually arrive at the output that I want?

Two models that fail in very different ways.

Suppose we have a chance that one piece in both model “breaks” and the downstream value of the break turns into a $1$. How many different ways can each model break? What would the output be for each of those breaks?

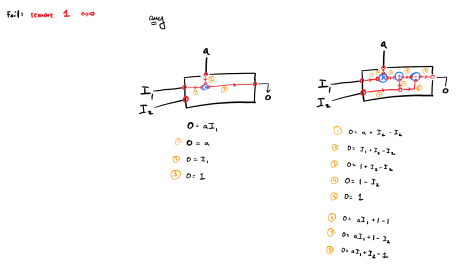
Looks like, very clearly, the two models “work” identically when things are fine, but when things start breaking they start looking very different. The fact that they don’t even have the same number of ways they can break is enough to say: yup, they’re not identical. But on top of that we see that the outputs that they give us are varying levels of useful and workable - in the real world some of these outputs aren’t mission failures. That matters a lot.

Summary

Understanding how a machine or model accomplishes its goal is very, very important in the real world because the real world often breaks foundational assumptions. This is obviously a simple example, but that should tell you how important this point is because this idea only expands in complex systems - there are many, many more ways a model can fail when it has more moving parts.

The key to confidence in my response is the mention of applicability. Application and dissonant assumptions are impossible to untangle - in other words, application always brings with it broken assumptions. Two models that accomplish the same output in an ideal situation are almost certainly going to fail in different ways ³.